Puzzle: We have a glass of milk and a bucket of water (Fig 1). First, we take a spoonful of milk from the glass and transfer it into the bucket. Next, we take a spoonful of the mixture from the bucket and transfer it back into the glass. Which will be greater, the amount of water in the glass or the milk in the bucket?
Fig 1 Glass of milk and bucket of water
Answer Equal
Solution The answer may seem surprising since we added a spoonful of milk to the bucket and less than a spoonful of water to the glass. However, the spoon with the mixture had also removed some milk from the bucket. This fact will equal the amount of foreign liquid in the containers (water in the glass and milk in the bucket).
Let the spoon with the mixture contain 1/3 water and 2/3 milk (Fig 2). We added 1/3 water to the glass. Yet, we also removed 2/3 milk from the bucket, leaving it with 1/3 milk. Consequently, both containers have an equal amount of foreign liquid: 1/3 water in the glass and 1/3 milk in the bucket.
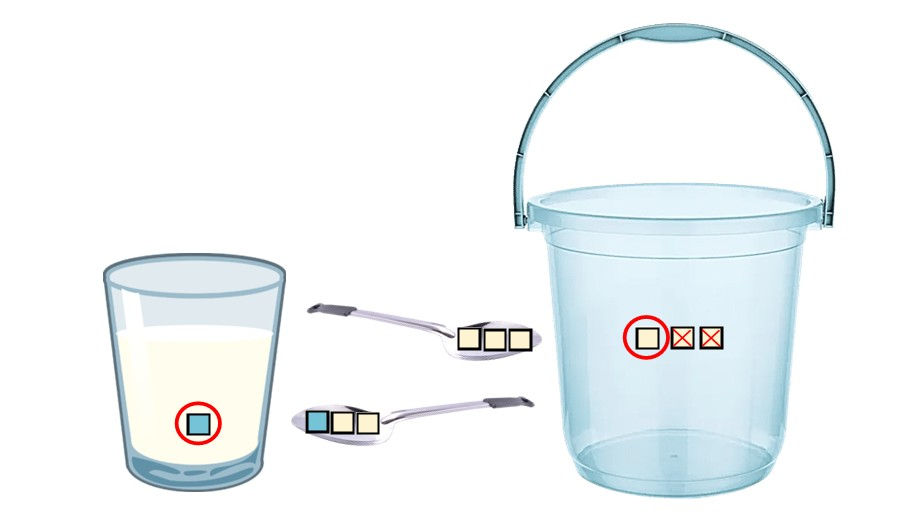
Fig 2 Glass of milk and bucket of water. The spoon contains 1/3 water and 2/3 milk.
Now, assume the spoon contains 6/7 water and 1/7 milk (Fig 3). We added 6/7 water to the glass and removed 1/7 milk from the bucket, leaving it with the 6/7 milk. Again, both containers will have an equal amount of foreign liquid: 6/7 water in the glass and 6/7 milk in the bucket.
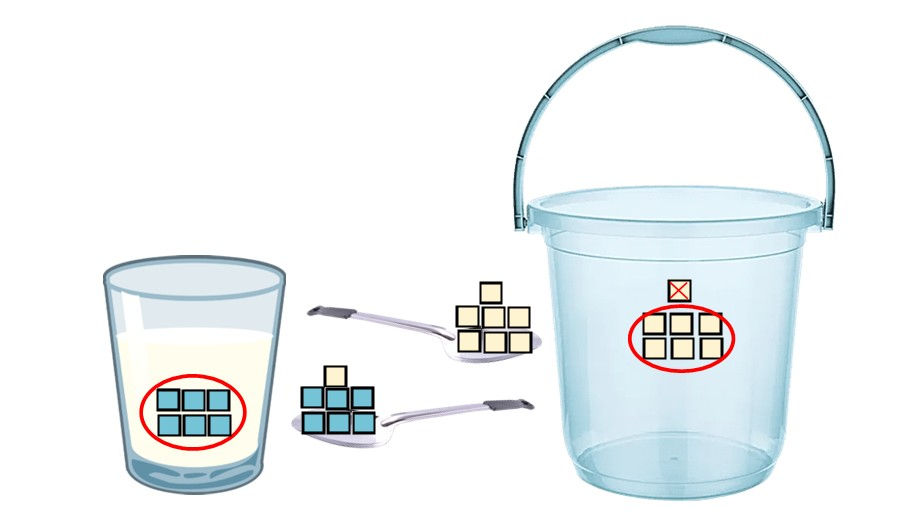
Fig 3 Glass of milk and bucket of water. The spoon contains 6/7 water and 1/7 milk.
It doesn't matter whether we stir the bucket or not; equality will be maintained in every situation:
If we scoop 1 spoonful of water from the bucket, leaving all milk there, we will end up with 1 spoonful of water in the glass and 1 spoonful of milk still left in the bucket. Equal.
If we scoop 0 water from the bucket (the spoon contains all the milk we put into the bucket), we end up with 0 water in the glass and 0 milk in the bucket. Equal.
The size of the containers is also irrelevant. The milk container can be larger, or they can be identical. The crucial factor is using one spoon for both transfers to ensure the amount of liquid exchanged remains constant. That is:
3/3 milk = 1 spoon = 1/3 water + 2/3 milk
and
7/7 milk = 1 spoon = 6/7 water + 1/7 milk
Comments